탐색 알고리즘2: 이진 탐색 (Binary Search)
1. 이진 탐색 (Binary Search) 이란?
- 탐색할 자료를 둘로 나누어 해당 데이터가 있을만한 곳을 탐색하는 방법
다음 문제를 먼저 생각해보자

이진 탐색의 이해 (순차 탐색과 비교하며 이해하기)
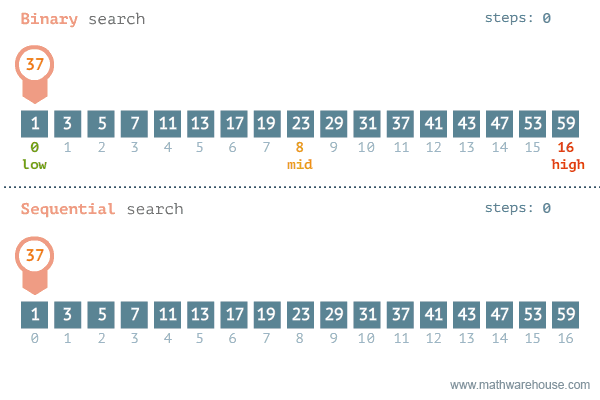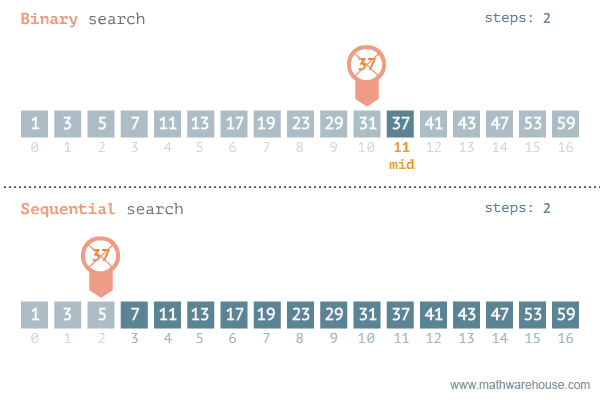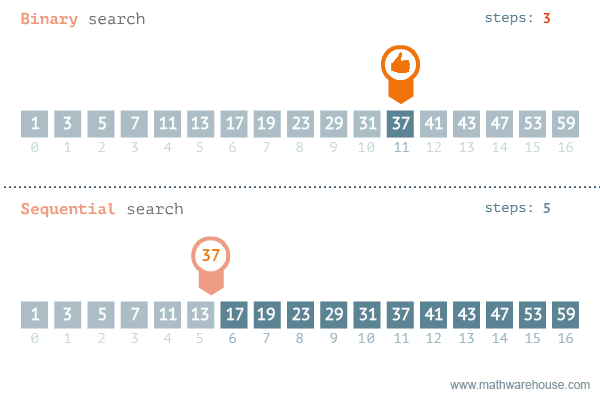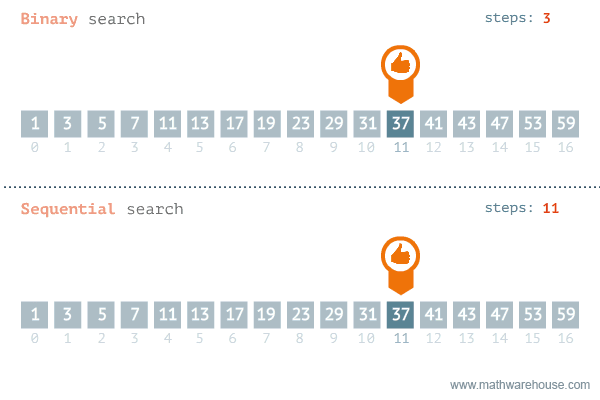
- [저작자] by penjee.com 이미지 출처
2. 분할 정복 알고리즘과 이진 탐색
- 분할 정복 알고리즘 (Divide and Conquer)
- Divide: 문제를 하나 또는 둘 이상으로 나눈다.
- Conquer: 나눠진 문제가 충분히 작고, 해결이 가능하다면 해결하고, 그렇지 않다면 다시 나눈다.
- 이진 탐색
- Divide: 리스트를 두 개의 서브 리스트로 나눈다.
- Comquer
- 검색할 숫자 (search) > 중간값 이면, 뒷 부분의 서브 리스트에서 검색할 숫자를 찾는다.
- 검색할 숫자 (search) < 중간값 이면, 앞 부분의 서브 리스트에서 검색할 숫자를 찾는다.
3. 어떻게 코드로 만들까?
- 이진 탐색은 데이터가 정렬되있는 상태에서 진행
- 데이터가 [2, 3, 8, 12, 20] 일 때,
- binary_search(data_list, find_data) 함수를 만들고
- find_data는 찾는 숫자
- data_list는 데이터 리스트
- data_list의 중간값을 find_data와 비교해서
- find_data < data_list의 중간값 이라면
- 맨 앞부터 data_list의 중간까지 에서 다시 find_data 찾기
- data_list의 중간값 < find_data 이라면
- data_list의 중간부터 맨 끝까지에서 다시 find_data 찾기
- 그렇지 않다면, data_list의 중간값은 find_data 인 경우로, return data_list 중간위치
- find_data < data_list의 중간값 이라면
- binary_search(data_list, find_data) 함수를 만들고
4. 알고리즘 구현
def binary_search(data, search):
print (data)
if len(data) == 1 and search == data[0]:
return True
if len(data) == 1 and search != data[0]:
return False
if len(data) == 0:
return False
medium = len(data) // 2
if search == data[medium]:
return True
else:
if search > data[medium]:
return binary_search(data[medium+1:], search)
else:
return binary_search(data[:medium], search)
import random
data_list = random.sample(range(100), 10)
data_list
output: [69, 65, 18, 71, 11, 10, 42, 68, 36, 89]
data_list.sort()
data_list
output: [10, 11, 18, 36, 42, 65, 68, 69, 71, 89]
binary_search(data_list, 66)
output:
[10, 11, 18, 36, 42, 65, 68, 69, 71, 89]
[68, 69, 71, 89]
[68, 69]
[68]
False5. 알고리즘 분석
- n개의 리스트를 매번 2로 나누어 1이 될 때까지 비교연산을 k회 진행
- n X $\frac { 1 }{ 2 }$ X $\frac { 1 }{ 2 }$ X $\frac { 1 }{ 2 }$ ... = 1
- n X $\frac { 1 }{ 2 }^k$ = 1
- n = $2^k$ = $log_2 n$ = $log_2 2^k$
- $log_2 n$ = k
- 빅 오 표기법으로는 k + 1 이 결국 최종 시간 복잡도임 (1이 되었을 때도, 비교연산을 한번 수행)
- 결국 O($log_2 n$ + 1) 이고, 2와 1, 상수는 삭제 되므로, O($log n$)
프로그래밍 연습
다음 10000개의 데이터를 삽입 정렬, 퀵 정렬로 정렬하는 함수를 각각 만들어보고, 각각의 정렬 시간을 출력하기
데이터 셋
import random
data_list = random.sample(range(100000), 10000)
현재 시간 구하기
import datetime
print (datetime.datetime.now())
반응형
'Algorithm > 알고리즘 이론' 카테고리의 다른 글
| Chapter 17-1. 깊이우선탐색(DFS) (0) | 2020.07.22 |
|---|---|
| Chapter 16. 그래프 이해 (0) | 2020.07.22 |
| Chapter 15-1. 순차 탐색 (Sequential Search) (0) | 2020.07.20 |
| Chapter 14-2. 퀵 정렬 (quick sort) (0) | 2020.07.20 |
| Chapter 14-1. 병합 정렬 (merge sort) (0) | 2020.07.20 |
