대표적인 정렬4: 병합 정렬 (merge sort)
1. 병합 정렬 (merge sort)
- 재귀용법을 활용한 정렬 알고리즘
- 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
- 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.
- 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다.
직접 눈으로 보면 더 이해가 쉽다: https://visualgo.net/en/sorting

출처: 위키피디아
2. 알고리즘 이해
- 데이터가 네 개 일때 (데이터 갯수에 따라 복잡도가 떨어지는 것은 아니므로, 네 개로 바로 로직을 이해해보자.)
- 예: data_list = [1, 9, 3, 2]
- 먼저 [1, 9], [3, 2] 로 나누고
- 다시 앞 부분은 [1], [9] 로 나누고
- 다시 정렬해서 합친다. [1, 9]
- 다음 [3, 2] 는 [3], [2] 로 나누고
- 다시 정렬해서 합친다 [2, 3]
- 이제 [1, 9] 와 [2, 3]을 합친다.
- 1 < 2 이니 [1]
- 9 > 2 이니 [1, 2]
- 9 > 3 이니 [1, 2, 3]
- 9 밖에 없으니, [1, 2, 3, 9]
- 예: data_list = [1, 9, 3, 2]
3. 알고리즘 구현
- mergesplit 함수 만들기
- 만약 리스트 갯수가 한개이면 해당 값 리턴
- 그렇지 않으면, 리스트를 앞뒤, 두 개로 나누기
- left = mergesplit(앞)
- right = mergesplit(뒤)
- merge(left, right)
- merge 함수 만들기
- 리스트 변수 하나 만들기 (sorted)
- left_index, right_index = 0
- while left_index < len(left) or right_index < len(right):
- 만약 left_index 나 right_index 가 이미 left 또는 right 리스트를 다 순회했다면, 그 반대쪽 데이터를 그대로 넣고, 해당 인덱스 1 증가
- if left[left_index] < right[right_index]:
- sorted.append(left[left_index])
- left_index += 1
- else:
- sorted.append(right[right_index])
- right_index += 1
작은 부분부터 작성해서 하나씩 구현하기
프로그래밍 연습
어떤 데이터리스트가 있을 때 리스트를 앞뒤로 짜르는 코드 작성해보기 (일반화)
def split_func(data):
medium = int(len(data) / 2)
print (medium)
left = data[:medium]
right = data[medium:]
print (left, right)
split_func([1, 5, 3, 2, 4])
output:
2
[1, 5] [3, 2, 4]재귀용법 활용하기
프로그래밍 연습
다음 문장을 코드로 작성해보기 (merge함수는 아직은 없는 상태, 있다고만 가정)
- mergesplit 함수 만들기
- 만약 리스트 갯수가 한개이면 해당 값 리턴
- 그렇지 않으면, 리스트를 앞뒤, 두 개로 나누기
- left = mergesplit(앞)
- right = mergesplit(뒤)
- merge(left, right)
def mergesplit(data):
if len(data) <= 1:
return data
medium = int(len(data) / 2)
left = mergesplit(data[:medium])
right = mergesplit(data[medium:])
return merge(left, right)merge 함수 만들기
- 목표: left 와 right 의 리스트 데이터를 정렬해서 sorted_list 라는 이름으로 return 하기
- left와 right는 이미 정렬된 상태 또는 데이터가 하나임
프로그래밍 연습
- left 부터 하나씩 right과 비교
- left > right 이면, left 를 sorted_list에 넣고, 다음 left 리스트와 right 비교
- 그렇지않으면 반대로 하기
다음 경우만 프로그래밍으로 작성해보기
left = [0]
right = [3]
결과는 별도의 리스트 변수를 만들어 적은 숫자 순으로 순서대로 저장해서 리턴
- 그렇지않으면 반대로 하기
프로그래밍 연습
다음 경우만 프로그래밍으로 작성해보기
left = [0, 2]
right = [1]
결과는 별도의 리스트 변수를 만들어 적은 숫자 순으로 순서대로 저장해서 리턴
프로그래밍 연습
다음 경우만 프로그래밍으로 작성해보기
left = [0, 2]
right = [1, 3]
결과는 별도의 리스트 변수를 만들어 적은 숫자 순으로 순서대로 저장해서 리턴
프로그래밍 연습
left, right 리스트 변수의 데이터 수가 한 개에서 여러 개가 될 수 있을때 작성해보기(일반화)
- sorted_list 리스트 변수 선언하기
- left_index, right_index 를 0 으로 초기화 하기
- while left_index < len(left) or right_index < len(right) 이면,
- 만약 left_index >= len(left)이면, sorted_list 에 right[right_index] 를 추가하고, right_index 값을 1증가
- 만약 right_index >= len(right)이면, sorted_list 에 left[left_index] 를 추가하고, left_index 값을 1증가
- 만약 left[left_index] < right[right_index]이면, sorted_list 에 left[left_index] 를 추가하고, left_index 값을 1증가
- 위 세가지가 아니면, sorted_list 에 right[right_index] 를 추가하고, right_index 값을 1증가
def merge(left, right):
merged = list()
left_point, right_point = 0, 0
# case1 - left/right 둘다 있을때
while len(left) > left_point and len(right) > right_point:
if left[left_point] > right[right_point]:
merged.append(right[right_point])
right_point += 1
else:
merged.append(left[left_point])
left_point += 1
# case2 - left 데이터가 없을 때
while len(left) > left_point:
merged.append(left[left_point])
left_point += 1
# case3 - right 데이터가 없을 때
while len(right) > right_point:
merged.append(right[right_point])
right_point += 1
return merged최종코드
def merge(left, right):
merged = list()
left_point, right_point = 0, 0
# case1 - left/right 둘다 있을때
while len(left) > left_point and len(right) > right_point:
if left[left_point] > right[right_point]:
merged.append(right[right_point])
right_point += 1
else:
merged.append(left[left_point])
left_point += 1
# case2 - left 데이터가 없을 때
while len(left) > left_point:
merged.append(left[left_point])
left_point += 1
# case3 - right 데이터가 없을 때
while len(right) > right_point:
merged.append(right[right_point])
right_point += 1
return merged
def mergesplit(data):
if len(data) <= 1:
return data
medium = int(len(data) / 2)
left = mergesplit(data[:medium])
right = mergesplit(data[medium:])
return merge(left, right)Check
import random
data_list = random.sample(range(100), 10)
mergesplit(data_list)
output: [8, 12, 24, 40, 47, 70, 81, 87, 92, 96]4. 알고리즘 분석
- 알고리즘 분석은 쉽지 않음, 이 부분은 참고로만 알아두자.
- 다음을 보고 이해해보자
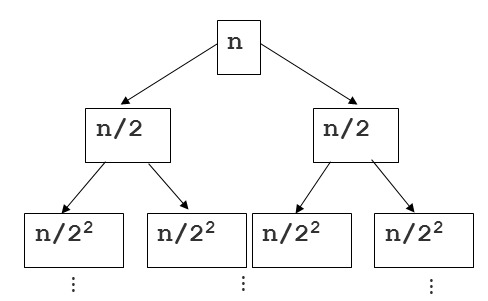
- 몇 단계 깊이까지 만들어지는지를 depth 라고 하고 i로 놓자. 맨 위 단계는 0으로 놓자.
- 다음 그림에서 n/$2^2$ 는 2단계 깊이라고 해보자.
- 각 단계에 있는 하나의 노드 안의 리스트 길이는 n/$2^2$ 가 된다.
- 각 단계에는 $2^i$ 개의 노드가 있다.
- 따라서, 각 단계는 항상 $2^i * \frac { n }{ 2^i } = O(n)$
- 단계는 항상 $log_2 n$ 개 만큼 만들어짐, 시간 복잡도는 결국 O(log n), 2는 역시 상수이므로 삭제
- 따라서, 단계별 시간 복잡도 O(n) * O(log n) = O(n log n)
- 몇 단계 깊이까지 만들어지는지를 depth 라고 하고 i로 놓자. 맨 위 단계는 0으로 놓자.
- 다음을 보고 이해해보자
프로그래밍 연습
지금 설명한 병합 정렬을 지금 다시 스스로 작성해보세요
728x90
'Algorithm > 알고리즘 이론' 카테고리의 다른 글
| Chapter 15-1. 순차 탐색 (Sequential Search) (0) | 2020.07.20 |
|---|---|
| Chapter 14-2. 퀵 정렬 (quick sort) (0) | 2020.07.20 |
| Chapter 13. 동적 계획법(Dynamic Programming)과 분할 정복 (Divide and Conquer) (0) | 2020.07.20 |
| Chapter 12. 재귀 용법(recursive call, 재귀 호출) (0) | 2020.07.20 |
| Chapter 11-3 선택 정렬 (selection sort) (0) | 2020.07.20 |