동적 계획법 (Dynamic Programming)과 분할 정복 (Divide and Conquer)
1. 정의
- 동적계획법 (DP 라고 많이 부름)
- 입력 크기가 작은 부분 문제들을 해결한 후, 해당 부분 문제의 해를 활용해서, 보다 큰 크기의 부분 문제를 해결, 최종적으로 전체 문제를 해결하는 알고리즘
- 상향식 접근법으로, 가장 최하위 해답을 구한 후, 이를 저장하고, 해당 결과값을 이용해서 상위 문제를 풀어가는 방식
- Memoization 기법을 사용함
- Memoization (메모이제이션) 이란: 프로그램 실행 시 이전에 계산한 값을 저장하여, 다시 계산하지 않도록 하여 전체 실행 속도를 빠르게 하는 기술
- 문제를 잘게 쪼갤 때, 부분 문제는 중복되어, 재활용됨
- 예: 피보나치 수열
- 분할 정복
- 문제를 나눌 수 없을 때까지 나누어서 각각을 풀면서 다시 합병하여 문제의 답을 얻는 알고리즘
- 하양식 접근법으로, 상위의 해답을 구하기 위해, 아래로 내려가면서 하위의 해답을 구하는 방식
- 일반적으로 재귀함수로 구현
- 문제를 잘게 쪼갤 때, 부분 문제는 서로 중복되지 않음
- 예: 병합 정렬, 퀵 정렬 등
2. 공통점과 차이점
- 공통점
- 문제를 잘게 쪼개서, 가장 작은 단위로 분할
- 차이점
- 동적 계획법
- 부분 문제는 중복되어, 상위 문제 해결 시 재활용됨
- Memoization 기법 사용 (부분 문제의 해답을 저장해서 재활용하는 최적화 기법으로 사용)
- 분할 정복
- 부분 문제는 서로 중복되지 않음
- Memoization 기법 사용 안함
- 동적 계획법
3. 동적 계획법 알고리즘 이해
프로그래밍 연습
피보나치 수열: n 을 입력받아서 다음과 같이 계산됨
n 을 입력받았을 때 피보나치 수열로 결과값을 출력하세요
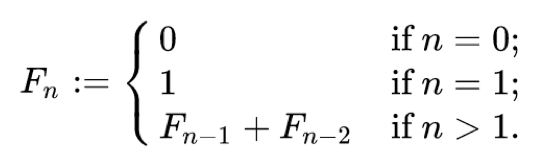
함수를 fibonacci 라고 하면,
fibonacci(0):0
fibonacci(1):1
fibonacci(2):1
fibonacci(3):2
fibonacci(4):3
fibonacci(5):5
fibonacci(6):8
fibonacci(7):13
fibonacci(8):21
fibonacci(9):34
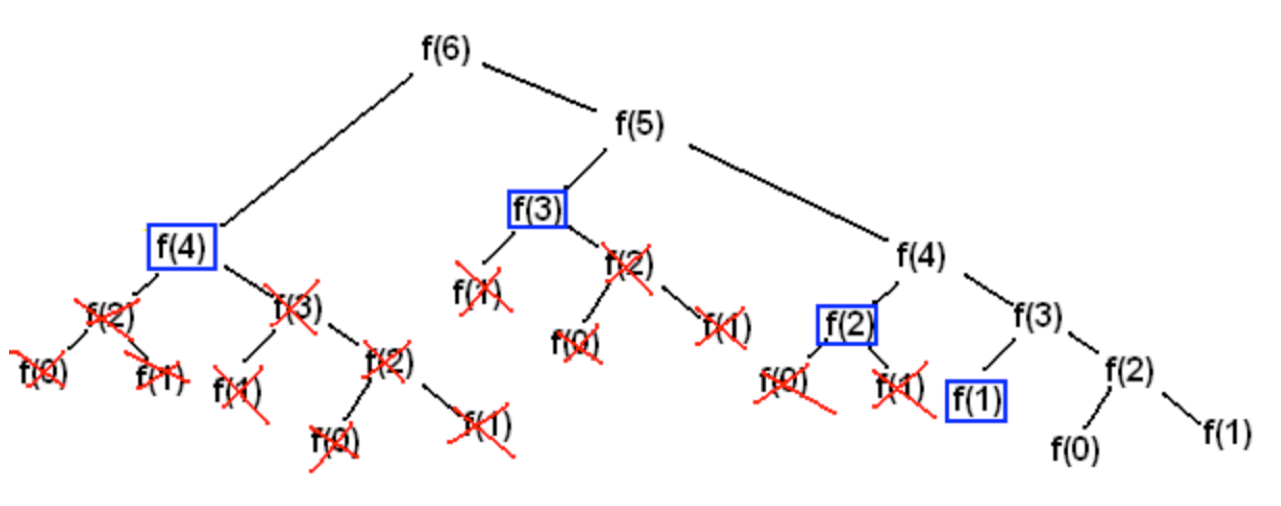
recursive call 활용
def fibo(num):
if num <= 1:
return num
return fibo(num - 1) + fibo(num - 2)
fibo(4)
output: 3동적 계획법 활용
def fibo_dp(num):
cache = [ 0 for index in range(num + 1)]
cache[0] = 0
cache[1] = 1
for index in range(2, num + 1):
cache[index] = cache[index - 1] + cache[index - 2]
return cache[num]
fibo(10)
output: 55실행 코드를 보며 이해해보기: 코드분석
분할 정복 알고리즘의 예는 별도 챕터에서 다루는 병합 정렬과 퀵 정렬을 통해 이해
반응형
'Algorithm > 알고리즘 이론' 카테고리의 다른 글
| Chapter 14-2. 퀵 정렬 (quick sort) (0) | 2020.07.20 |
|---|---|
| Chapter 14-1. 병합 정렬 (merge sort) (0) | 2020.07.20 |
| Chapter 12. 재귀 용법(recursive call, 재귀 호출) (0) | 2020.07.20 |
| Chapter 11-3 선택 정렬 (selection sort) (0) | 2020.07.20 |
| Chapter 11-2 삽입 정렬 (insertion sort) (0) | 2020.07.20 |